À la fin du 19ème siècle, une partie de la communauté scientifique s’enorgueillissait d’avoir résolu les mystères de notre monde. Elle était alors persuadée qu’il n’y avait plus grand chose à découvrir, seulement des problèmes mineurs qu’elle ne tarderait pas à résoudre.
Mais c’était sans compter, entre autres, sur l’épineux problème du décalage orbital de Mercure proche du soleil, que la mécanique newtonienne ne parvenait pas à modéliser.
En effet, par la mécanique newtonienne, nous pouvions prévoir le ballet des planètes et de leur(s) satellite(s) naturel(s) avec une très bonne précision. Cependant Mercure, la planète la plus proche du soleil, échappait aux prévisions du modèle newtonien. Il fallait donc concevoir une théorie, un modèle, intégrant les particularités orbitales de Mercure, tout en prédisant avec exactitude les mouvements des autres corps célestes.
Einstein et Hilbert
Au début du 20ème siècle, deux personnages de renom font l’actualité scientifique : le physicien théoricien Albert Einstein et le mathématicien David Hilbert. Les médias américains ont énormément contribué à faire d’Albert Einstein la movie star du monde de la physique théorique. Cela a engendré dans l’esprit du grand public, le sentiment que seul Einstein était en mesure de mener des calculs complexes, que personne ne pouvait comprendre. La réalité est tout autre.

David Hilbert, nouvellement imprégné par la théorie d’Einstein change totalement d’orientation. Muni d’un bagage mathématique conséquent, il va très rapidement rattraper Einstein en publiant le 20 novembre 1915 un premier article, aux annales de l’Académie scientifiques de Prusse intitulé « Les fondement de la physique ». Il tente, alors, de formuler une équation de champ qui contient à la fois la gravitation et l’électromagnétisme. Einstein, voyant la vitesse folle à laquelle avance Hilbert, publie seulement 5 jours plus tard dans la même revue, soit le 25 novembre 1915, un article évocateur intitulé « L’équation de champ de la gravitation » :
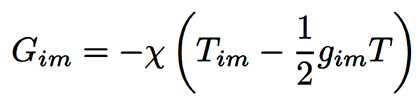
C’est cette équation qui continue de guider, encore aujourd’hui, la cosmologie contemporaine. Mais le 18 novembre 1915, soit une semaine auparavant, Einstein avait publié une solution de l’équation de champ. Bizarre me direz-vous, comment peut-on publier une solution d’équation sans l’équation ? Il s’agissait d’une description de la gravitation dans le vide (à l’extérieur d’une étoile par exemple) qui lui permettait de rendre compte du décalage orbital de Mercure.
David Hilbert ne tardera pas à féliciter son précieux rival par le biais d’une lettre. Il lui demandera alors comment il a fait, pour parvenir aussi vite, à formuler son équation de champ. Einstein, ne donnera pas suite à cette correspondance…
Erreur d’interprétation de l’équation de Schwarzschild
Parallèlement à cette confrontation scientifique, un autre mathématicien du nom de Karl Schwarzschild s’engage dans l’armée allemande sur le front russe. Il prend alors connaissance de la solution linéaire de l’équation de champ d’Albert Einstein. Aussitôt, Karl Schwarzschild s’empresse de dresser une solution, non linéaire, plus sophistiquée de cette équation. Il la publiera, le 13 janvier 1916 sous le titre « À propos du champ gravitationnel d’un point de masse selon la théorie d’Einstein ». (Annales de l’Académie des sciences de Prusse).
Par son équation, Karl Schwarzschild va parvenir à décrire la gravité à l’extérieur d’une étoile. Cependant, les coordonnées utilisées dans sa solution ne sont pas les mêmes que celles d’Einstein. Karl Schwarzschild utilise dans son équation « une grandeur intermédiaire » nommée « R ».
Définition de « R » : Il s’agit du rayon « r » d’un cercle ou d’une sphère, auquel on ajoute une constante (a). Donc, la valeur « R » pour Schwarzschild se traduit ainsi R = r + a.
Cette variable d’espace « R » va être interprétée, par le mathématicien David Hilbert, comme une simple « distance radiale » nommée « r » en physique. La distance radiale est le rayon d’un cercle ou d’une sphère nommé « r ». Ainsi, Hilbert se trompe en écrivant « r » (rayon) au lieu de « R » égal à (r + a).

Cette confusion va engendrer un travestissement total des équations de Schwarzschild. Jusqu’à aujourd’hui, cela a entraîné une confusion dans tous les livres de cosmologie qui reproduisent cette erreur d’interprétation depuis 1916.
La conception théorique des trous noirs est issue de cette erreur d’interprétation des équations de Schwarschild par Hilbert.
L’existence des trous noirs faussement fondée mathématiquement, alimentera bien des articles comme ceux que publieront Stephen Hawking et Roger Penrose…
Comment une telle erreur physico-mathématique a-t-elle pu durer un siècle ?
La réponse est déconcertante. En 1916, la circulation de l’information scientifique était aux antipodes de celle d’aujourd’hui, la photocopieuse et internet n’existaient pas !
La communauté scientifique, dans sa grande majorité, n’a pas pris connaissance des articles originaux de Schwarzschild et pour cause, elle ne lit pas l’allemand. Le premier article, du 13 janvier 1916 ne sera traduit en anglais qu’en 1975 et le second en 1999.
Il est intéressant de faire remarquer, que des tentatives d’éclaircissements ont tout de même émergé mais n’ont pas eu d’écho. On peut citer l’article du mathématicien Leonard S. Abrams publié en 1989 au journal canadien de physique sous le titre, très révélateur « trous noirs : l’héritage de l’erreur commise par Hilbert ». Ce mathématicien est malheureusement décédé la même année.
On peut citer également, le physicien théoricien italien, Salvatore Antoci qui a publié en 2003 et 2011 des articles reprenant une argumentation similaire à celle de Abrams. Ses articles n’eurent aucun impact sur la remise en question de l’existence des trous noirs au sein de la communauté scientifique.
Il est essentiel de rappeler que nous devons l’ensemble de ces mises au point scientifiques, toutes ces informations et tous ces éclaircissements, au physicien Jean Pierre Petit. La théorie des trous noirs étant obsolète et définitivement enterrée, peut-être allons nous enfin pouvoir parler de cosmologie gémellaire, seule cosmologie digne d’intérêt aujourd’hui.
Tarik Imine (physicien)
Pour en savoir plus : version complète scientifique publiée sur phosphenia.com ci-dessous :
https://phosphenia.com/wp-content/uploads/2018/01/Article-Trou-Noir.pdf
voir également : www.jp-petit.org/papers/cosmo
Morphéus N°85 janvier février 2018



